Boolean Algebra

Due: 11:00pm, Thursday October 29, 2020

Max grace days: 2

Problems

Problem 1

Find the output of the following circuit:

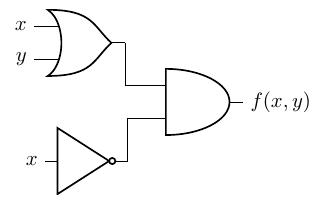
Problem 2

Find the output of the following circuit:

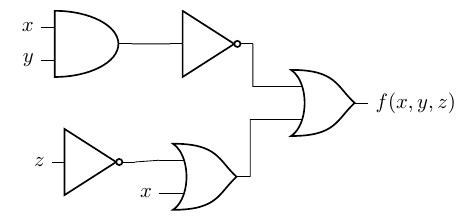
Problem 3

Draw a circuit for the function f(x, y, z) = x ⋅ y + x ⋅ z + y ⋅ z

Problem 4

Rewrite a + b using only NOT and two-input NAND.

Problem 5

Determine the input conditions for the following circuit so that f(a, b, c) = 1

Problem 6

Show that
$$\overline{a} \cdot \overline{c} + a \cdot \overline{c} + b \cdot c = b + \overline{c}$$

Problem 7

Simplify
$$f(a, b, c) = a \cdot b + a \cdot c + c + \overline{a} \cdot b \cdot \overline{c}$$

Problem 8

Use a Karnaugh map to reduce
$$f(a, b, c, d) = \overline{a} \cdot \overline{b} + a \cdot \overline{b} + \overline{c} \cdot \overline{d} + c \cdot \overline{d}$$
to a minimum sum of products form.

Problem 9

Design a circuit that takes a 4-bit binary number and produces 1 if the number is greater than twelve or less than three. Show the truth table, logic minimization and circuit diagram.

Problem 10

Design a circuit that takes a digit encoded as a 4-bit binary number and produces 1 if the number is greater than or equal to five. Show the truth table, Karnaugh map and circuit diagram. Note the Karnaugh map will have don’t care conditions for non-digit values.

Turning in the Assignment

Submit a single file containing your answers to the problems to the appropriate folder on D2L.

Grading Criteria

10 points per problem