Logic Design

References

• Slides adapted from CMU

Outline

• Introduction to binary logic gates
• Truth table construction
• Logic functions and their simplifications
• Laws of binary logic

Overview of Logic Design

• Fundamental Hardware Requirements
  • Communication (how to get values from one place to another)
  • Computation
  • Storage
• Bits
  • Everything expressed in terms of values 0 and 1
  • Communication: low or high voltage on wire
  • Computation: compute with Boolean functions
  • Storage: store bits of information

Digital Signals

• Use voltage thresholds to extract discrete values from continuous signal.
• Simplest version: 1-bit signal
  • Either high range (1) or low range (0)
  • With guard range between them
• Not strongly affected by noise or low quality circuit elements
  • Can make circuits simple, small and fast

Semiconductors to Computers

• Increasing levels of complexity
  • Transistors built from semiconductors
  • Logic gates built from transistors
  • Logic functions built from gates
  • Flip-flops built from logic
  • Counters and sequencers from flip-flops
  • Microprocessors from sequencers
  • Computers from microprocessors

Semiconductors to Computers

• Increasing levels of Abstraction
  • Physics
  • Transistors
  • Gates (this lecture)
  • Logic (this lecture)
  • Microprogramming
  • Assembler
  • Programming languages
  • Applications

Logic Gates

• Basic logic circuits with one or more inputs and one output are called gates
• Gates are used as the building blocks in the design of more complex digital logic circuits.

Representing Logic Functions

• There are several ways of representing logic functions:
  • Symbols to represent the gates
  • Truth tables
  • Boolean algebra

NOT Gate

• Truth table

  a	y
  0	1
  1	0

• Boolean algebra

  \[y = \overline{a}\]

AND Gate

• Truth table

  a	b	y
  0	0	0
  0	1	0
  1	0	0
  1	1	1

• Boolean algebra

  \[y = a \cdot b\]

OR Gate

• Truth table

  a	b	y
  0	0	0
  0	1	1
  1	0	1
  1	1	1

• Boolean algebra

  \[y = a + b\]

XOR Gate

• Truth table

  a	b	y
  0	0	0
  0	1	1
  1	0	1
  1	1	0

• Boolean algebra

  \[y = a \oplus b\]

NOT AND (NAND) Gate

• Truth table

  a	b	y
  0	0	1
  0	1	1
  1	0	1
  1	1	0

• Boolean algebra

  \[y = \overline{a \cdot b}\]

NOT OR (NOR) Gate

• Truth table

  a	b	y
  0	0	1
  0	1	0
  1	0	0
  1	1	0

• Boolean algebra

  \[y = \overline{a + b}\]

Boolean Algebra

• Boolean algebra can be used to design combinational logic circuits

• OR
  • \(a + 0 = a\)
  • \(a + a = a\)
  • \(a + 1 = 1\)
  • \(a + \overline{a} = 1\)
• AND
  • \(a \cdot 0 = 0\)
  • \(a \cdot a = a\)
  • \(a \cdot 1 = a\)
  • \(a \cdot \overline{a} = 0\)

Boolean Algebra Properties

• Commutation
  • \(a + b = b + a\)
  • \(a \cdot b = b \cdot a\)
• Association
  • \((a + b) + c = a + (b + c)\)
  • \((a \cdot b) \cdot c = a \cdot (b \cdot c)\)
• Distribution
  • \(a \cdot (b + c) = (a \cdot b) + (a \cdot c)\)
  • \(a + (b \cdot c) = (a+b) \cdot (a+c)\)
• Absorption
  • \(a + (a \cdot c) = a\)
  • \(a \cdot (a+c) = a\)

Boolean Algebra Example

• Simplify

  \[ \begin{align*} & x \cdot y + \overline{y} \cdot z + x \cdot z + x \cdot y \cdot z \\ & x \cdot y \cdot z + x \cdot y \cdot \overline{z} + x \cdot \overline{y} \cdot z + \overline{x} \cdot \overline{y} \cdot z + x \cdot y \cdot z + x \cdot \overline{y} \cdot z + x \cdot y \cdot z \\ & x \cdot y \cdot z + x \cdot y \cdot \overline{z} + x \cdot \overline{y} \cdot z + \overline{x} \cdot \overline{y} \cdot z \\ & x \cdot y \cdot (z + \overline{z}) + \overline{y} \cdot z \cdot (x + \overline{x}) \\ & x \cdot y \cdot 1 + \overline{y} \cdot z \cdot 1\\ & x \cdot y + \overline{y} \cdot z \end{align*} \]

DeMorgan’s Theorem

• \(\overline{a + b + c + \ldots} = \overline{a} \cdot \overline{b} \cdot \overline{c} \cdot \ldots\)
• \(\overline{a \cdot b \cdot c \cdot \ldots} = \overline{a} + \overline{b} + \overline{c} + \ldots\)

• Proof for \(\overline{a + b} = \overline{a} \cdot \overline{b}\)

  \(a\)	\(b\)	\(\overline{a + b}\)	\(\overline{a} \cdot \overline{b}\)
  0	0	1	1
  0	1	0	0
  1	0	0	0
  1	1	0	0

DeMorgan’s Example

• Simplify

  \[ \begin{align*} & a \cdot \overline{b} + a \cdot (\overline{b + c}) + b \cdot (\overline{b + c})\\ & a \cdot \overline{b} + a \cdot \overline{b} \cdot \overline{c} + b \cdot \overline{b} \cdot \overline{c}\\ & a \cdot \overline{b} + a \cdot \overline{b} \cdot \overline{c}\\ & a \cdot \overline{b} \end{align*} \]

DeMorgan’s in Gates

• The function \(f = a \cdot b + c \cdot d\) can be implemented with AND and OR gates

DeMorgan’s in Gates

• Two consecutive NOT gates cancel out.

DeMorgan’s in Gates

• The function \(f = a \cdot b + c \cdot d\) can be simplified to use only NAND gates.

Logic Minimisation

• Any Boolean function can be implemented directly using combinational logic
• Simplifying the Boolean function will reduce the number of gates required to implement the function
• Logic minimization techniques:
  • Algebraic manipulation
  • Karnaugh (K) mapping (visual approach)
  • Tabular approaches (for example Quine-McCluskey)
• Karnaugh mapping is usually preferred for up to about 5 variables

Truth Tables

• \(f\) is defined by the following truth table

  x	y	z	f	minterms
  0	0	0	1	\(\overline{x} \cdot \overline{y} \cdot \overline{z}\)
  0	0	1	1	\(\overline{x} \cdot \overline{y} \cdot z\)
  0	1	0	1	\(\overline{x} \cdot y \cdot \overline{z}\)
  0	1	1	1	\(\overline{x} \cdot y \cdot z\)
  1	0	0	0
  1	0	1	0
  1	1	0	0
  1	1	1	1	\(x \cdot y \cdot z\)

• A minterm must contain all variables (in either complemented or uncomplemented form)

Disjunctive Normal Form

• A Boolean function expressed as the disjunction (OR) of its minterms is said to be in the Disjunctive Normal Form (DNF)

• Example:

  \[f = \overline{x} \cdot \overline{y} \cdot \overline{z} + \overline{x} \cdot \overline{y} \cdot z + \overline{x} \cdot y \cdot \overline{z} + \overline{x} \cdot y \cdot z + x \cdot y \cdot z\]

• A Boolean function expressed as the ORing of ANDed variables (not necessarily minterms) is in Sum of Products (SOP) form.

  \[f = \overline{x} + y \cdot z\]

Maxterms

• A maxterm of \(n\) Boolean variables is the disjunction of all the variables either in complemented or uncomplemented form.

• Example (referring to the truth table for \(f\))

  \[\begin{align*} \overline{f} &= x \cdot \overline{y} \cdot \overline{z} + x \cdot \overline{y} \cdot z + z \cdot y \cdot \overline{z}\\ f &= (\overline{x} + y + z) \cdot (\overline{x} + y + \overline{z}) \cdot (\overline{x} + \overline{y} + z) \end{align*}\]

  • The maxterms of \(f\) are effectively the minterms of \(\overline{f}\) with each variable complemented.

Conjunctive Normal Form

• A Boolean function expressed as the conjunction (AND) of its maxterms is said to be in Conjunctive Normal Form (CNF)

• Example:

  \[f = (\overline{x} + y + z) \cdot (\overline{x} + y + \overline{z}) \cdot (\overline{x} + \overline{y} + z)\]

• A Boolean function expressed as the ANDing of ORed variables (not necessarily maxterms) is often said to be in Product of Sums (POS) form.

Logic Simplification

• Boolean algebra can be used to simplify logical expressions.
• Note: the DNF and CNF are not simplified
• There is a technique called Karnaugh mapping that is sometimes easier (for humans to do)

Karnaugh Maps

• Karnaugh Maps (or K-maps) are a powerful visual tool for carrying out simplification and manipulation of logical expressions with less than 6 variables.

• The K-map is a rectangular array of cells
  • Each possible state of the input variables corresponds uniquely to one of the cells
  • The corresponding output state is written in each cell

K-map Example

• Simplify:

  \[f = \overline{x} \cdot \overline{y} \cdot \overline{z} + \overline{x} \cdot \overline{y} \cdot z + \overline{x} \cdot y \cdot \overline{z} + \overline{x} \cdot y \cdot z + x \cdot y \cdot z\]

• K-map:

  

K-map Example

• Group terms
  • With size equal to a power of 2
  • Large groups best since they contain fewer variables
  • Groups can wrap around edges and corners

  

• Simplified: \(f = \overline{x} + y \cdot z\)

K-map Example

• Plot \(f = \overline{a} \cdot b + b \cdot \overline{c} \cdot \overline{d}\)

  

• In a 4 variable map:
  • 1 variable term occupies 8 cells
  • 2 variable terms ocuppy 4 cells
  • 3 variable terms occupy 2 cells, etc.

K-map Example

• Plot \(f = \overline{b}\)

  

• Plot \(f = \overline{b} \cdot \overline{d}\)

  

K-map Example

• Simplify \(f = \overline{a} \cdot b \overline{d} + b \cdot c \cdot d + \overline{a} \cdot b \cdot \overline{c} \cdot d + c \cdot d\)

  

• \(f = \overline{a} \cdot b + c \cdot d\)

POS Simplification

• Note that the previous examples yielded simplified expressions in the SOP form
  • Suitable for implementations using AND followed by OR gates, or only NAND gates
• Sometimes we may wish to get a simplified expression in POS form
  • Suitable for implementations using OR followed by AND gates, or only NOR gates
• To do this we group zeros in the map, then apply DeMorgan’s and complement

POS Example

• Simplify \(f = \overline{a} \cdot b + b \cdot \overline{c} \cdot \overline{d}\) into POS form

  

• Simplified: \(\overline{f} = \overline{b} + a \cdot c + a \cdot d\)

• Applying DeMorgan’s: \(f = b \cdot ( \overline{a} + \overline{c}) \cdot (\overline{a} + \overline{d})\)

Expressions in POS Form

• Apply DeMorgan’s and take the complement, that is, \(\overline{f}\) is now in SOP form

• Fill in zeros in table, that is, plot \(\overline{f}\)

• Fill remaining cells with ones, that is, plot \(f\)

• Simplify in the usual way by grouping ones to simplify \(f\)

Don’t Care Conditions

• Sometimes we do not care about the output value of a combinational logic circuit, for example, if certain input combinations can never occur.

• These are called don’t care conditions

• In a simplification they may be treated as 0 or 1 depending on which gives the simplest result

Don’t Care Conditions Example

• Simplify the function \(f = \overline{a} \cdot \overline{b} \cdot d + \overline{a} \cdot c \cdot d + a \cdot c \cdot d\) with don’t care conditions \(\overline{a} \cdot \overline{b} \cdot \overline{c} \cdot \overline{d}\), \(\overline{a} \cdot \overline{b} \cdot c \cdot \overline{d}\), \(\overline{a} \cdot b \cdot \overline{c} \cdot d\)

  

• Simplified: \(f = \overline{a} \cdot \overline{b} + c \cdot d\) or \(f = \overline{a} \cdot d + c \cdot d\)

K-map Definitions

• Cover - a term is said to cover a minterm if that minterm is part of that term

• Prime implicant - a term that cannot be further combined

• Essential term - a prime implicant that covers a minterm that no other prime implicant covers

• Covering set - a minimum set of prime implicants which includes all essential terms plus any other prime implicants required to cover all minterms

Combinational Circuit Example

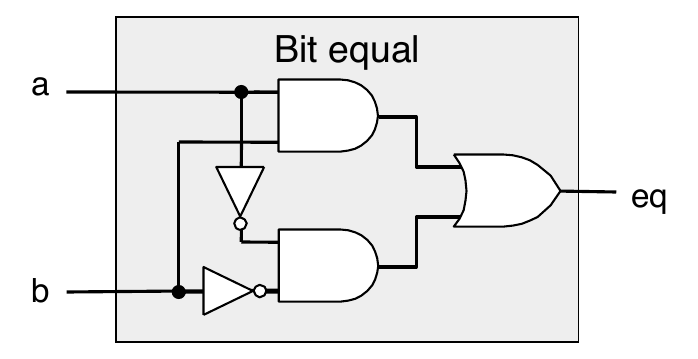
• Truth table

  \(a\)	\(b\)	\(out\)
  0	0	1
  0	1	0
  1	0	0
  1	1	1

Half Adder

• Adds two single bit binary numbers \(a\) and \(b\) (note: no carry input)

• Truth table

  \(a\)	\(b\)	\(c_{out}\)	\(sum\)
  0	0	0	0
  0	1	0	1
  1	0	0	1
  1	1	1	0

Full adder

• Adds two single bit numbers \(a\) and \(b\) (note: with a carry input)

• Truth table

  \(c_{in}\)	\(a\)	\(b\)	\(c_{out}\)	\(sum\)
  0	0	0	0	0
  0	0	1	0	1
  0	1	0	0	1
  0	1	1	1	0
  1	0	0	0	1
  1	0	1	1	0
  1	1	0	1	0
  1	1	1	1	1

Ripple Carry Adder

• The half adder and full adder implement two bit binary addition with and without carry-in

• In general, we need to add two \(n\) bit binary numbers

• The ripple carry adder is \(n\) full adders cascaded together.

• Example: 4 bit adder

  

  • Note: if \(a\) is complemented and \(c_0\) set to 1, then the operation is: \(s = b - a\)

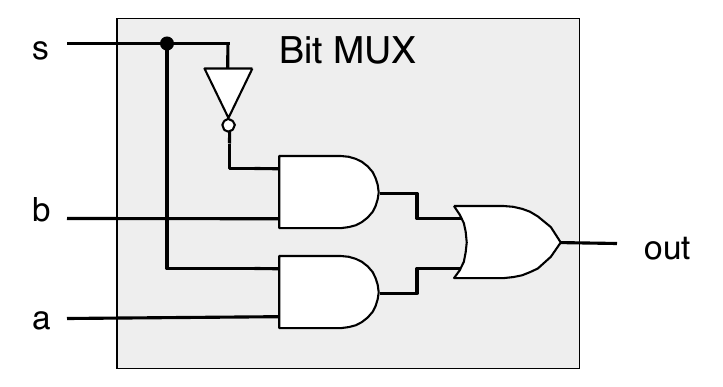
Bit-Level Multiplexor

• A bit-level multiplexor has data signals \(a\) and \(b\) and a control signal \(c\) outputs \(a\) or \(b\) depending on \(c\)

• Truth table

  \(a\)	\(b\)	\(c\)	out
  0	0	0	0 (b)
  0	0	1	0 (a)
  0	1	0	1 (b)
  0	1	1	0 (a)
  1	0	0	0 (b)
  1	0	1	1 (a)
  1	1	0	1 (b)
  1	1	1	1 (a)

Bit-Level Multiplexor

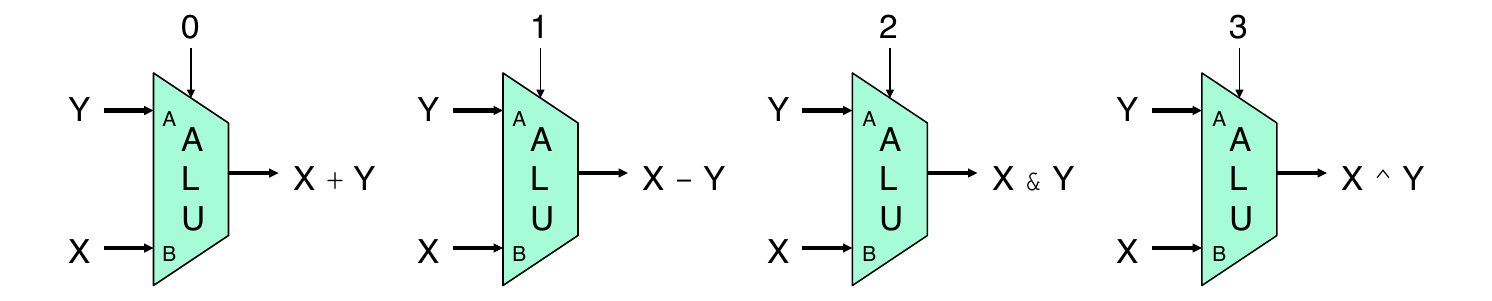
Arithmetic Logic Unit

• Combinational logic – a more complex version of a multiplexor
• Control signal selects function computed

• Also computes condition codes

• Example: four function ALU

  

Memory Elements

• Sequential logic has a memory
• A memory stores data
• The snapshot of the memory is called the state
• A one bit memory is called bistable, that is, it has two internal states
• Flip-flops and latches are implementations of bistables

RS Latch

• An RS latch is a memory element with two inputs: reset (\(R\)) and set (\(S\)), and two outputs: \(Q\) and \(\overline{Q}\)

  \(S\)	\(R\)	\(Q'\)	\(\overline{Q'}\)	comment
  0	0	\(Q\)	\(\overline{Q}\)	hold
  0	1	0	1	reset
  1	0	1	0	set
  1	1	0	0	illegal

where \(Q'\) is the next state and \(Q\) is the current state.

RS Latch

RS Latch State Transition Table

• A state transition table is a way of viewing the operation of an RS latch.

  \(Q\)	\(S\)	\(R\)	\(Q'\)	comment
  0	0	0	0	hold
  0	0	1	0	reset
  0	1	0	1	set
  0	1	1	0	illegal
  1	0	0	1	hold
  1	0	1	0	reset
  1	1	0	1	set
  1	1	1	0	illegal

Clocks and Synchronous Circuits

• The RS latch output state changes occur directly in response to changes in the inputs. This is called asynchronous operation.

• Most sequential circuits employ synchronous operation.
  • The output is constrained to change only at a time specified by a global enabling signal
  • This signal is generally called the system clock

• The clock is typically a square wave signal at a particular frequency that imposes order on the state changes.

Gated RS Latch

• The RS latch can be modified to only change state when a valid enable signal (such as from the system clock) is present.

Registers

• Store a word of data
  • Different from program registers seen in assembly code
• Collection of edge-triggered latches (one for every bit in word)
• Loads input on rising edge of clock

Register Operation

• Stores data bits
• Generally acts as a barrier between input and output
• As clock rises, loads input

State Machine Example

• Accumulator circuit
  • Load or accumulate on each cycle

Random-Access Memory

• Stores multiple words of memory
  • Address input specifies which word to read or write
• Register file
  • Holds values of program registers

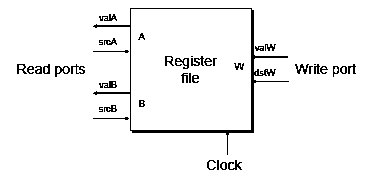
Register File Timing

• Reading
  • Like combinational logic
  • Output generated based on input address (after some delay)
• Writing
  • Like register
  • Update only as clock rises

Summary

• Computation
  • Performed by combinational logic
  • Computes Boolean functions
  • Continuously reacts to input changes
• Storage
  • Registers
    • Hold single words
    • Loaded as clock rises
  • Random-access memories
    • Hold multiple words
    • Can have multiple read or write ports
    • Read a word when address input changes
    • Write word as clock rises