Bits, Bytes and Integers
CSC 235 - Computer Organization
References
- Slides adapted from CMU
Outline
Representing information as bits
Bit-level manipulations
Integers
Representation: unsigned and signed
Conversion, casting
Expanding, truncating
Addition, negation, multiplication, shifting
Summary
Representations in memory, pointers, strings
Everything is bits
Each bit is 0 or 1
By encoding/interpreting sets of bits in various ways
Computers determine what to do (instructions)
… and represent and manipulate numbers, sets, strings, etc.
Why bits? Electronic implementation
Easy to store with bitstable elements
Reliably transmitted on noisy and inaccurate wires
Example: Counting in Binary
Base 2 number representation
Represent \(15213_{10}\) as \(11101101101101_{2}\)
Represent \(1.20_{10}\) as \(1.0011001100110011[0011] \ldots_{2}\)
Represent \(1.5213 \times 10^4\) as \(1.1101101101101_{2} \times 2^{13}\)
Encoding Byte Values
Byte = 8 bits
Binary: \(00000000_{2}\) to \(11111111_{2}\)
Decimal: \(0_{10}\) to \(255_{10}\)
Hexadecimal: \(00_{16}\) to \(FF_{16}\)
Base 16 number representation
Use characters ‘0’ to ‘9’ and ‘A’ to ‘F’
Typically written in most programming languages with the prefix
0x
Encoding Byte Values
| Hex | Decimal | Binary |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
Encoding Byte Values
| Hex | Decimal | Binary |
|---|---|---|
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 1100 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
Example Data Representations
| C Data | Typical 32-bit | Typical-64 | x86-64 |
|---|---|---|---|
char |
1 | 1 | 1 |
short |
2 | 2 | 2 |
int |
4 | 4 | 4 |
long |
4 | 8 | 8 |
float |
4 | 4 | 4 |
double |
8 | 8 | 8 |
| pointer | 4 | 8 | 8 |
Boolean Algebra
Algebraic representation of logic
Encode “true” as 1 and “false” as 0
Developed by George Boole in the 19th Century
Operations
and (
&):a & b = 1when botha = 1andb = 1or (
|):a | b = 1when eithera = 1andb = 1not (
~):~a = 1whena = 0xor (
^):a ^ b = 1when eithera = 1orb = 1, but not both
General Boolean Algebras
Operate on Bit Vectors
- operations applied bitwise
Example: \[\begin{align*} & 01101001\\ \texttt{&} \; & 01010101\\ \hline & 01000001\\ \end{align*}\]
All of the properties of Boolean algebra apply
Example: Representing and Manipulating Sets
Representation
Width \(w\) bit vector represents subsets of \(\{0, \ldots, w-1\}\)
\(a_j = 1\) if \(j \in A\)
Operations
&: intersection|: union^: symmetric difference~: complement
Example: Representing and Manipulating Sets
Examples with \(w = 8\)
\(x = 01101001 = \{0, 3, 5, 6\}\)
\(y = 01010101 = \{0, 2, 4, 6\}\)
\(x \; \texttt{&} \; y = 01000001 = \{0, 6\}\)
\(x \; \texttt{|} \; y = 01111101 = \{0, 2, 3, 4, 5, 6\}\)
Bit-Level Operations in C
The operations
&,|,~, and^are available in Capply to any “integral” data type:
long,int,short,char,unsignedarguments are viewed as bit vectors
arguments are applied bitwise
Examples with
chartype~0x41\(\rightarrow\)0xBE~0x00\(\rightarrow\)0xFF0x69 & 0x55\(\rightarrow\)0x41
Contrast: Logical Operations in C
The logical operations in C are
&&,||, and!zero is viewed as “false”
any non-zero value is viewed as “true”
always return 0 or 1
short-circuit evaluation
Examples with
chardata type!0x41\(\rightarrow\)0x00!0x00\(\rightarrow\)0x010x42 && 0x55\(\rightarrow\)0x01
Shift Operations
Left shift:
x << yshift bit vector
xleftypositionsfill with zeros on the right
Right shift:
x >> yshift bit vector
xrightypositionslogical shift: fill with zeros on the left
arithmetic shift: replicate most significant bit on the left
Undefined behavior: shift amount less than zero or greater than bit vector length
Shift Examples
x = 01100010x << 3 = 00010000logical:
x >> 2 = 00011000arithmetic:
x >> 2 = 00011000
x = 10100010x << 3 = 00010000logical:
x >> 2 = 00101000arithmetic:
x >> 2 = 11101000
Encoding Integers
Unsigned
\[B2U(x) = \sum_{i=0}^{w-1} x_i \cdot 2^i\]
where \(x\) is the bit vector and \(w\) is the length of the bit vector
Signed: two’s complement
\[B2T(x) = -x_{w-1} \cdot 2^{w-1} \sum_{i=0}^{w-2} x_i \cdot 2^i\]
where \(x\) is the bit vector, \(w\) is the length of the bit vector, and \(-x_{x-1}\) is the sign bit
Example 3 Bit Integer Encodings
| value | unsigned | two’s complement |
|---|---|---|
000 |
(0+0+0) = 0 |
(0+0+0) = 0 |
001 |
(0+0+1) = 1 |
(0+0+1) = 1 |
010 |
(0+2+0) = 2 |
(0+2+0) = 2 |
011 |
(0+2+1) = 3 |
(0+2+1) = 3 |
100 |
(4+0+0) = 4 |
(-4+0+0) = -4 |
101 |
(4+0+1) = 5 |
(-4+0+1) = -3 |
110 |
(4+2+0) = 6 |
(-4+2+0) = -2 |
111 |
(4+2+1) = 7 |
(-4+2+1) = -1 |
Numeric Ranges
Unsigned values
min = 0
max = \(2^{w} - 1\)
Two’s complement values
min = \(-2^{w-1}\)
max = \(2^{w-1} - 1\)
Example Numeric Ranges
Values where \(w = 16\)
decimal hex binary unsigned max 65535 FF FF 11111111 11111111 signed max 32767 7F FF 01111111 11111111 signed min -32768 80 00 10000000 00000000 -1 -1 FF FF 11111111 11111111 0 0 00 00 00000000 00000000
Unsigned and Signed Numeric Values
Equivalence
- Same encodings for non-negative values
Uniqueness
Every bit pattern represents a unique integer value
Each representable integer has a unique bit encoding
Can invert mappings
unsigned bit pattern = \(U2B(x) = B2U^{-1}(x)\)
two’s complement bit pattern = \(T2B(x) = B2T^{-1}(x)\)
Mapping Between Signed and Unsigned
Mappings between unsigned and two’s complement numbers: keep the bit representation and reinterpret.
Two’s complement to unsigned: \(T2B \circ B2U\)
Unsigned to two’s complement: \(U2B \circ B2T\)
Signed to Unsigned
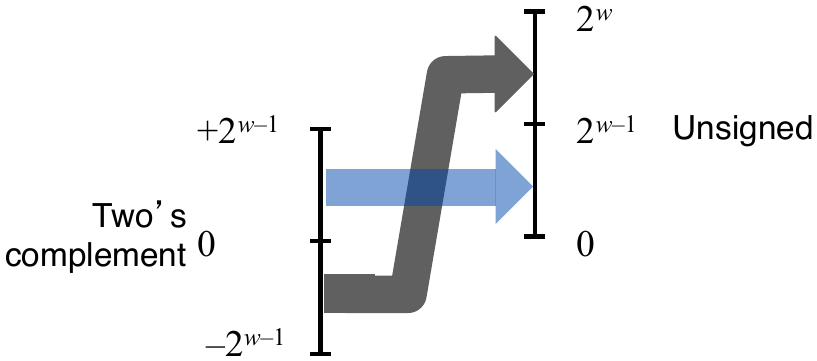
Unsigned to Signed
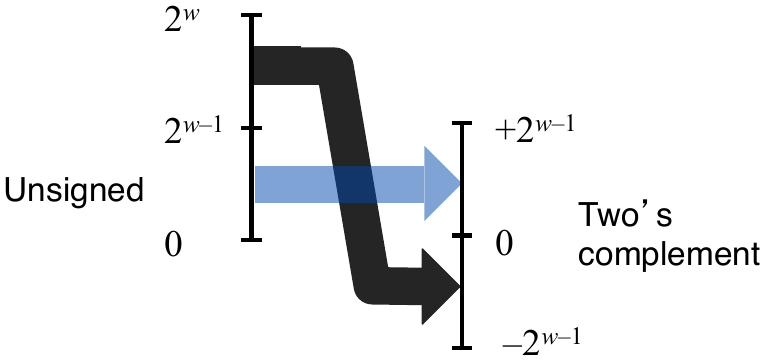
Signed vs. Unsigned in C
Constants
By default are considered to be signed integers
Unsigned if the suffix is “U”, for example
42U
Casting
Explicit casting between signed and unsigned same as \(U2T\) and \(T2U\)
Implicit casting also occurs via assignments and procedure calls
Casting Surprises
Expression evaluation
If there is a mix of unsigned and signed integers in a single expression, then signed values are implicilty cast to unsigned values.
Including comparison operations:
<, >, ==, <=, >=
Examples
Operand 1 Operand 2 Relation Evaluation 0 0U == unsigned -1 0 < signed -1 0U > unsigned -1 -2 > signed
Unsigned vs. Signed in C
Easy to make mistakes
Example 1
unsigned i; for (i = cnt-2; i >= 0; i--) a[i] += a[i+1]Example 2
#define DELTA sizeof(int) int i; for (i = CNT; i-DELTA >= 0; i -= DELTA) ...
Summary: Casting Rules
Bit pattern is maintained, but reinterpreted
Can have unexpected effects: adding or subtracting \(2^w\)
An expression containing signed and unsigned
ints implicitly casts the signedints to unsignedints
Sign Extension
Task
Given \(w\)-bit signed integer \(x\)
Convert it to \(w+k\) bit integer \(x'\) with the same value
Rule
Make \(k\) copies of the sign bit:
\(x' = x_{w-1}, \ldots, x_{w-1}, x_{w-1}, x_{w-2}, \ldots, x_{0}\)
C automatically performs sign extension
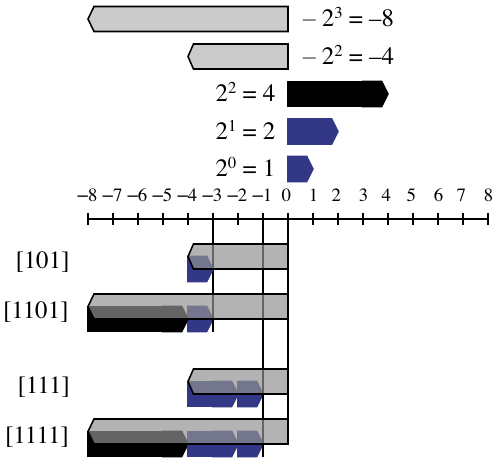
Sign Extension Example
Example of sign extensions from \(w=3\) to \(w=4\)
![Sign Extension]()
Sign Extension
Truncation
Task:
Given \(k+w\)-bit signed or unsigned integer \(x\)
Convert it to \(w\)-bit integer \(x'\) with the same value for “small enough” \(x\)
Rule:
Drop top \(k\) bits:
\(x' = x_{w-1}, x_{w-2}, \ldots, x_0\)
Summary: Expanding and Truncating Rules
Expanding (e.g.
shorttoint)Unsigned: zeros added
Signed: sign extension
Both yield expected result
Truncating (e.g.
inttoshort)Unsigned/signed: bits are truncated
Result is reinterpreted
Unsigned: modulus operation
Signed: similar to modulus
For small (in magnitude) numbers yields expected behavior
Unsigned Addition
\(UAdd_{w}(u, v)\)
Operands: \(w\) bits
True sum: \(w+1\) bits
Discard carry: \(w\) bits
Standard addition function ignores carry output
Implements modular arithmetic
\[s = UAdd_w(u, v) = u + v \; \texttt{mod} \; 2^w\]
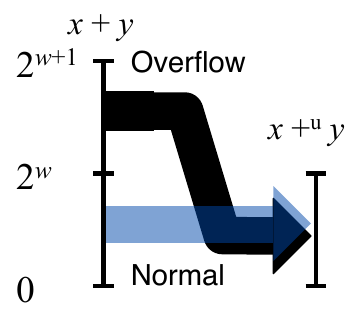
\(UAdd\) Overflow
Implements modular arithmetic \(s = UAdd_w(u, v) = u + v \; \texttt{mod} \; 2^w\)
![Unsigned Integer Overflow]()
Unsigned Integer Overflow
Visualizing Mathematical Integer Addition
\(Add_4(u, v)\)
![Integer Addition]()
Integer Addition
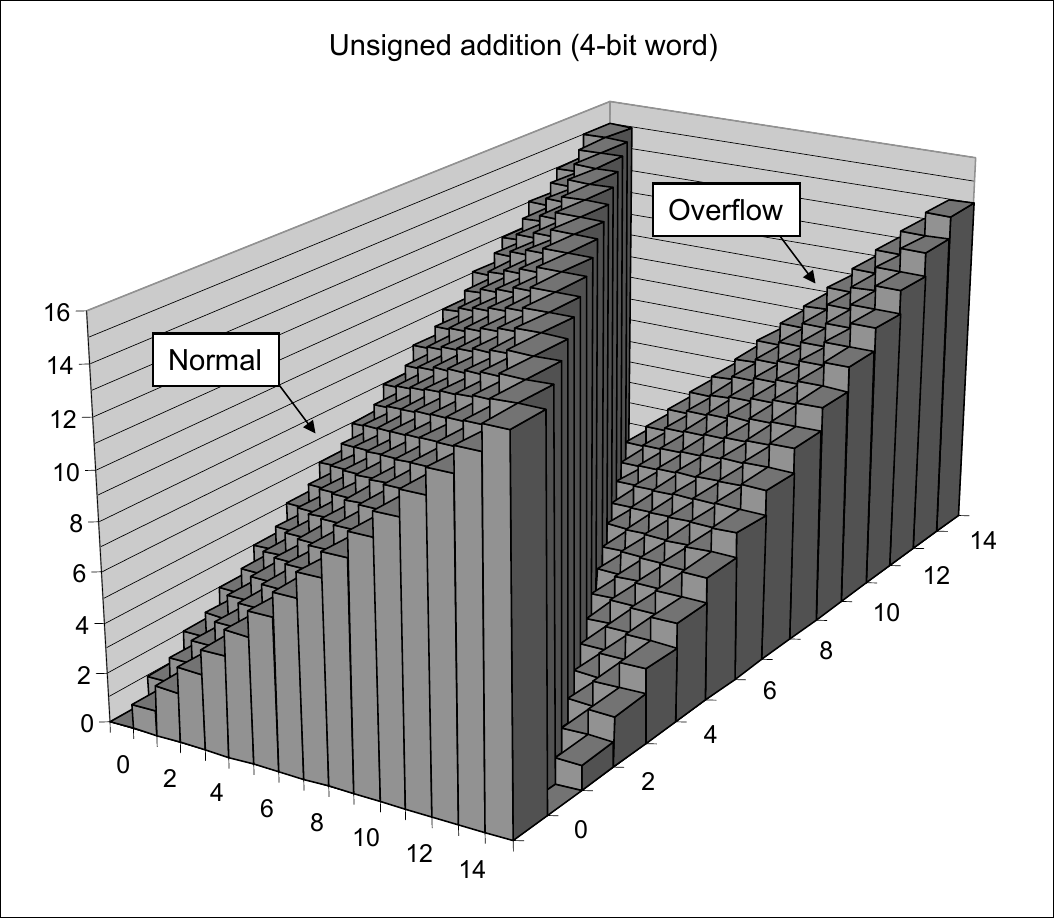
Visualizing Unsigned Integer Addition
\(UAdd_4(u, v)\)
![Unsigned Integer Addition]()
Unsigned Integer Addition
Two’s Complement Addition
\(TAdd_{w}(u, v)\)
Operands: \(w\) bits
True sum: \(w+1\) bits
Discard carry: \(w\) bits
\(TAdd\) and \(Uadd\) have identical bit level behavior
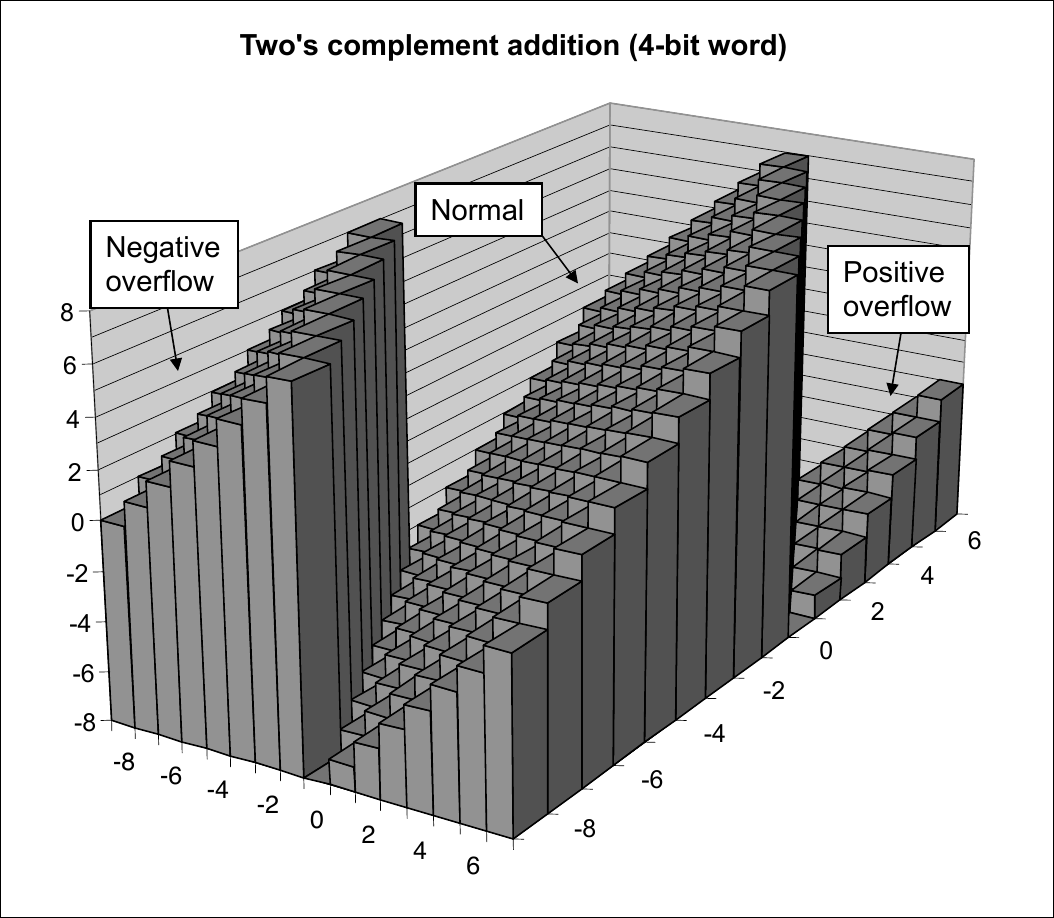
\(TAdd\) Overflow
True add requires \(w+1\) bits; drop off the most significant bit and interpret as 2’s complement integer
![Signed Integer Overflow]()
Signed Integer Overflow
Visualizing Two’s Complement Addition
\(TAdd_{4}(u, v)\)
![Signed Integer Addition]()
Signed Integer Addition
Integer Multiplication
Problem: the exact product of \(w\)-bit numbers \(u, v\) might have a result that exceeds \(w\) bits.
Unsigned: up to \(2w\) bits
Two’s complement min (negative): up to \(2w-1\) bits
Two’s complement max (positive): up to \(2w\) bits
Maintaining exact results
would need to keep expanding word size with each product computed
is done in software if needed
Unsigned Multiplication in C
\(UMul_{w}(u, v)\)
Operands: \(w\) bits
True product: \(2w\) bits
Discard \(w\) bits: \(w\) bits
Implements modular arithmetic
\[s = UMul_w(u, v) = u + v \; \texttt{mod} \; 2^w\]
Signed Multiplication in C
\(TMul_{w}(u, v)\)
Operands: \(w\) bits
True product: \(2w\) bits
Discard \(w\) bits: \(w\) bits
Ignores high order \(w\) bits, some of which are different for signed vs. unsigned multiplication
Power-of-2 Multiply with Shift
Operation
u << kGives \(u \cdot 2^k\) for both signed and unsigned
Operands: \(w\) bits
True product \(w+k\) bits
Discard \(k\) bits: \(w\) bits
Unsigned Power-of-2 Divide with Shift
Operation
u >> kGives
\[\bigg\lfloor \frac{u}{2^k} \bigg\rfloor\]
Uses logical shift
Signed Power-of-2 Divide with Shift
Operation
u >> kGives
\[\bigg\lfloor \frac{u}{2^k} \bigg\rfloor\]
Uses arithmetic shift
Rounds wrong direction when \(u < 0\)
Correct Signed Power-of-2 Divide with Shift
Quotient of negative number power of 2
Want
\[\bigg\lceil \frac{u}{2^k} \bigg\rceil\]
Compute as
\[\bigg\lfloor \frac{u+2^k-1}{2^k} \bigg\rfloor\]
In C:
(u + (1<<k) - 1) >> kBiases dividend toward 0
Negation: Complement and Increment
Negate through complement and increment
~x + 1 = -xExamples
Value x~x~x+1Result 15213 3B6DC492C493-15213 0 0000FFFF00000 TMin 80007FFF8000TMin
Arithmetic: Basic Rules
Addition
Unsigned/signed: normal addition followed by truncate
Unsigned: addition
mod\(2^w\)Signed: modified addition
mod\(2^w\) (result in proper range)
Multiplication
Unsigned/signed: normal multiplication followed by truncate
Unsigned: multiplication
mod\(2^w\)Signed: modified multiplication
mod\(2^w\) (result in proper range)
Byte-Oriented Memory Organization
Programs refer to data by address
Conceptually envision it as a very large array of bytes
An address is like an index into that array, and a pointer variable stores an address
Note: system provides private address space to each “process”
Think of a process as a program being executed
So, a program can clobber its own data, but not that of others
Machine Words
Any given computer has a “word size”
- Nominal size of integer-valued data
Until recently, most machines used 32 bits (4 bytes) as a word size
Increasingly, machines have 64 bit word size
Machines still support multiple data formats
Fractions or multiples of word size
Always integral number of bytes
Word-Oriented Memory Organization
Addresses specify byte locations
Address of first byte in word
Addresses of successive words differ by 4 (32 bit) or 8 (64 bit)
Byte Ordering
How are the bytes within a multi-byte word ordered in memory?
Conventions
Big endian: least significant byte has highest address
Little endian: least significant byte has lowest address
Example: 4-byte value of
0x1234567Big endian:
01 23 45 67Little endian:
67 45 23 01
Examining Data Representations
Code to print byte representation of data
typedef unsigned char *pointer; void show_bytes(pointer start, size_t len) { size_t i; for (i = 0; i < len; i++) { printf("%p\t0x%.2x\n", start+i, start[i]); } printf("\n"); }
Representing Strings
Strings in C
Represented by an array of characters
Each character is encoded in ASCII format
Strings should be null terminated (final character = 0)
Compatibility
- Byte ordering is not an issue
Reading Byte-Reversed Listings
Disassembly
Text representation of binary machine code
Generated by program that reads the machine code
Example Fragment
Address Instruction code Assembly Rendition 8048365: 5b pop 8048366: 81 c3 ab 12 00 00 add $0x12ab,%ebx 804836c: 83 bb 28 00 00 00 00 cmpl $0x0,0x28(%ebx)
Summary
Representing information as bits
Bit-level manipulations
Integers
Representation: unsigned and signed
Conversion, casting
Expanding, truncating
Addition, negation, multiplication, shifting
Summary
Representations in memory, pointers, strings