Cache Memories

CSC 235 - Computer Organization

References

  • Slides adapted from CMU

Outline

  • Cache memory organization and operation
  • Performance impact of caches
    • The memory mountain
    • Rearranging loops to improve spatial locality
    • Using blocking to improve temporal locality

Recall: Locality

  • Principle of Locality: Programs tend to use data and instructions with addresses near or equal to those they have used recently

  • Temporal locality:
    • Recently referenced items are likely to be referenced again in the near future
  • Spatial locality:
    • Items with nearby addresses tend to be referenced close together in time

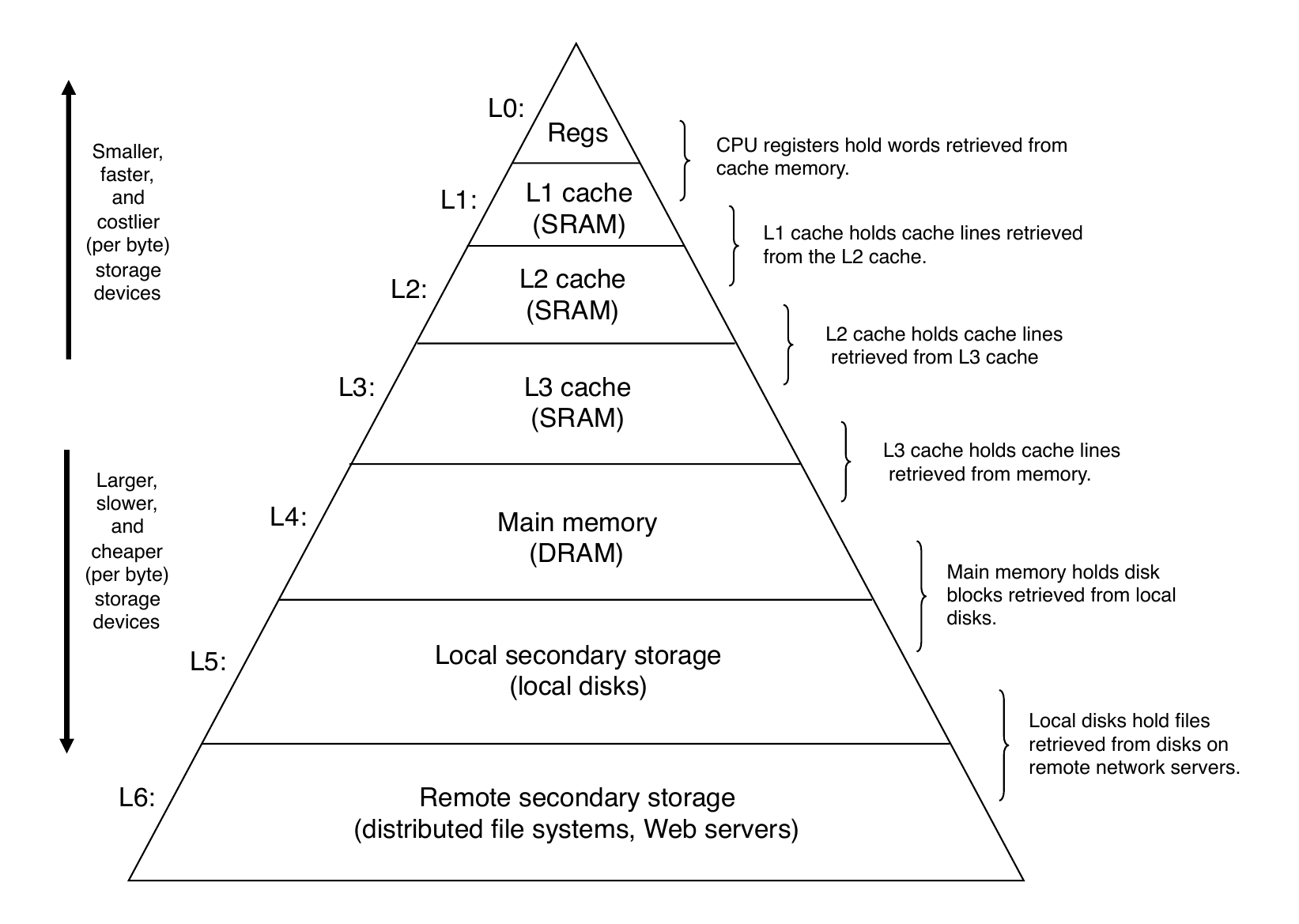
Recall: Memory Hierarchy

Memory Hierarchy
Memory Hierarchy

Recall: General Cache Concepts

Cache Concepts
Cache Concepts

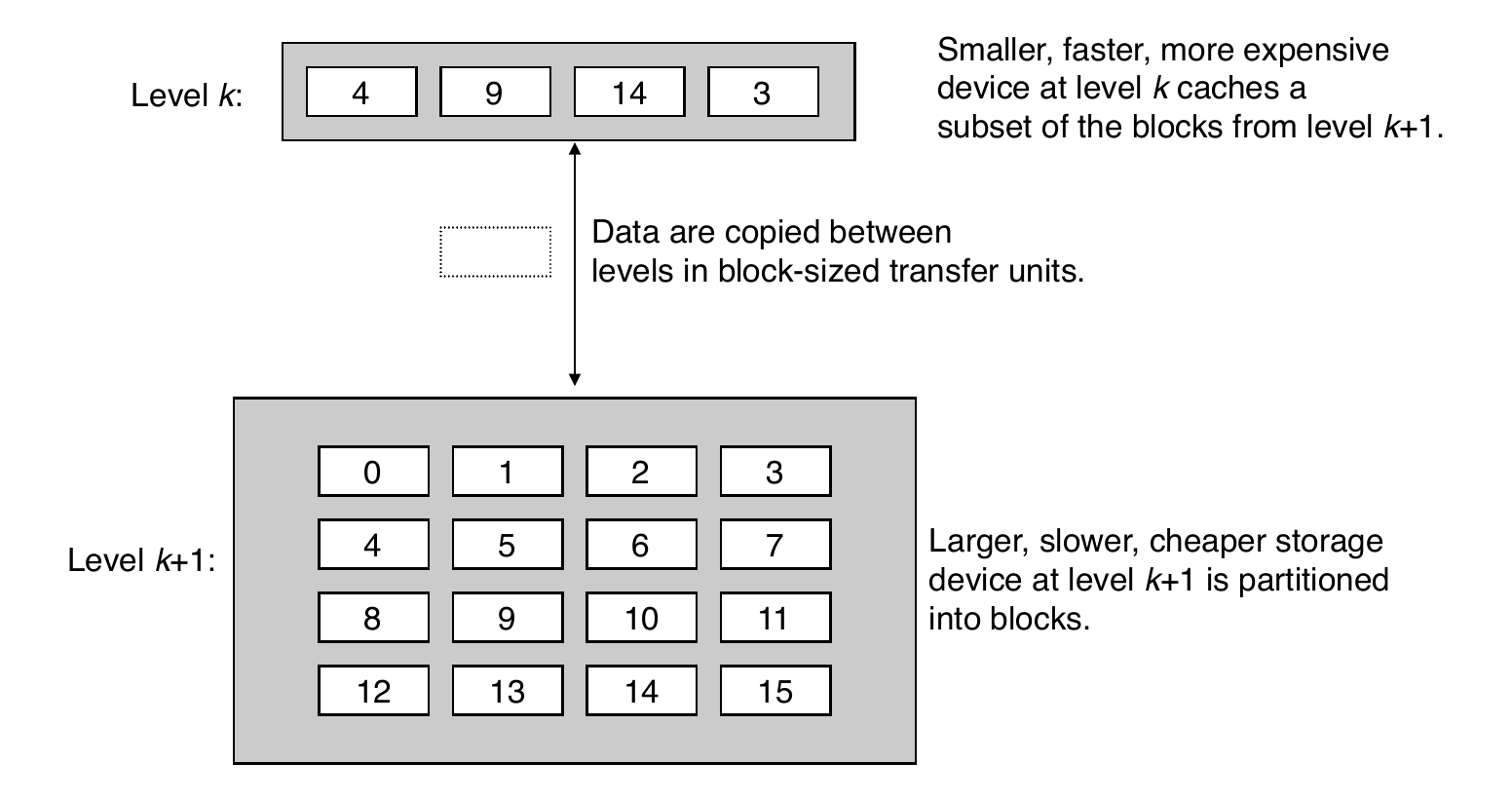
Recall: General Cache Concepts

  • A cache hit is when the data in block \(b\) is needed and is in the cache

  • A cache miss is when the data in block \(b\) is needed and is in not the cache

  • Types of cache misses:
    • Cold (compulsory) miss: occur because the cache starts empty and this is the first reference to the block
    • Capacity miss: occur when the set of active cache blocks (working set) is larger than the cache
    • Conflict miss: occur when the level \(k\) cache is large enough, but multiple data objects all map to the same level \(k\) block where a block is a small subset of the block positions at level \(k-1\)

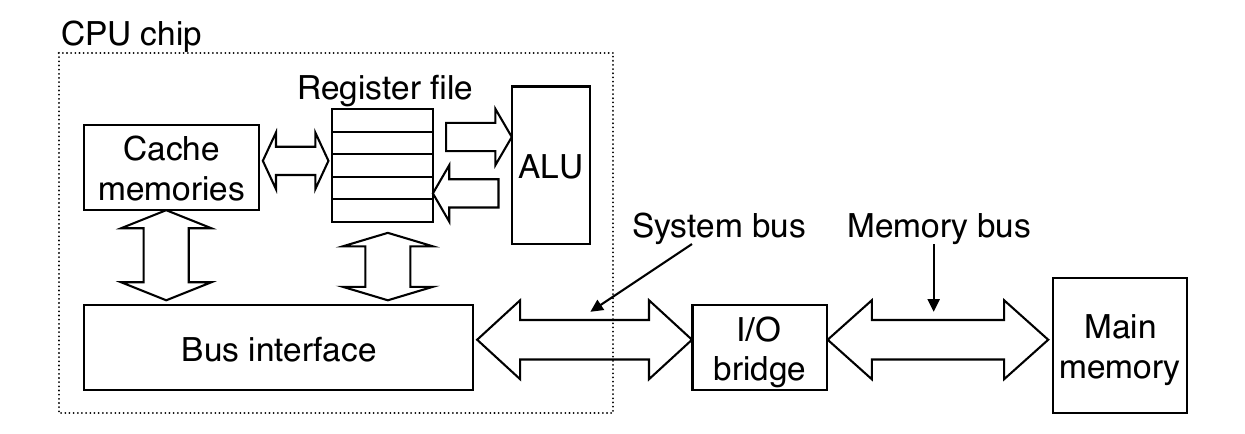
Cache Memories

  • Cache memories are small, fast SRAM-based memories managed automatically in hardware
    • Hold frequently accessed blocks of main memory

  • CPU looks first for data in cache

  • Typical system structure:

Cache Bus
Cache Bus

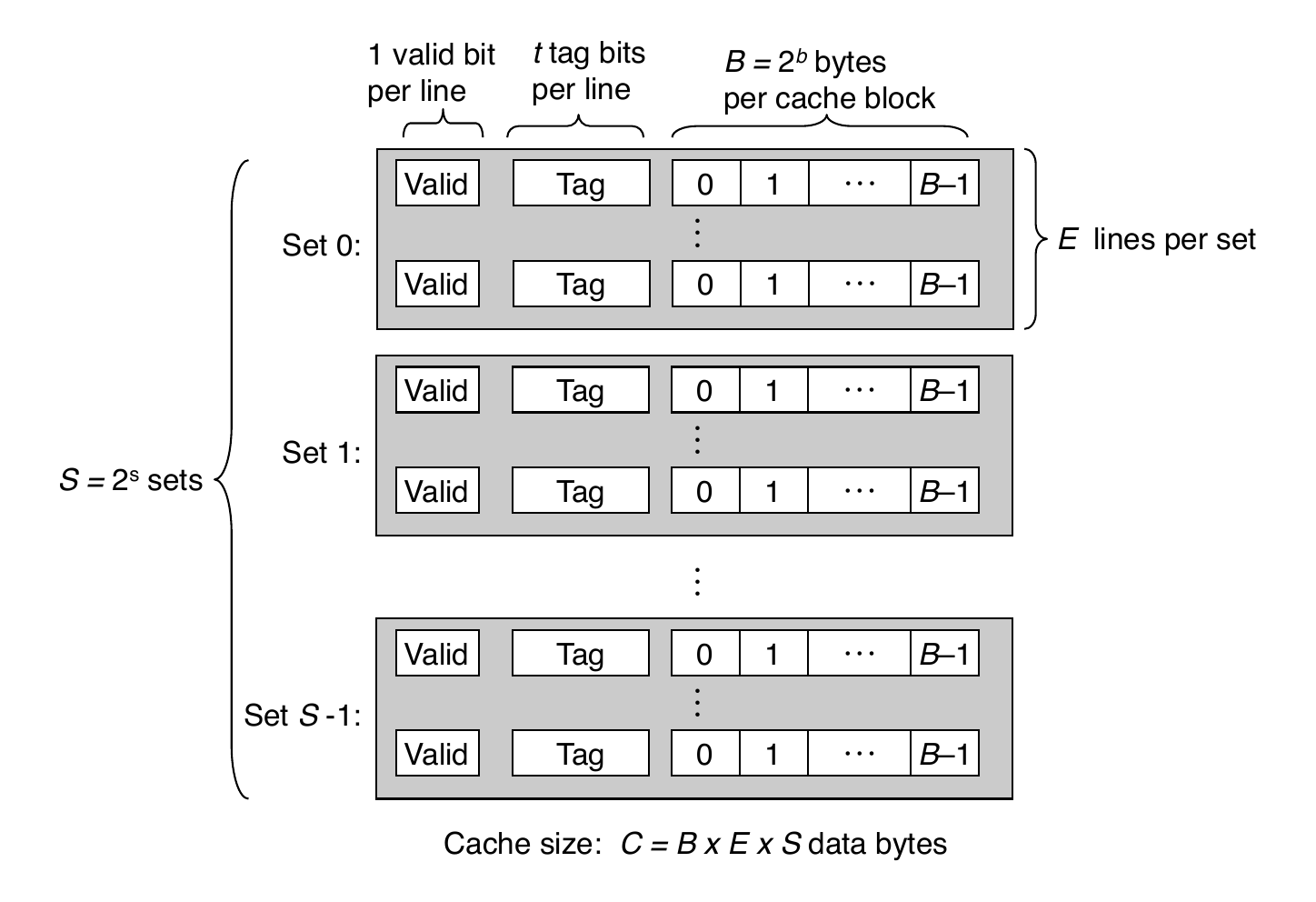
General Cache Organization (S, E, B)

Cache Organization
Cache Organization

Cache Read

  • Locate set

  • Check if any line in set has matching tag

  • Yes and the line is valid: hit

  • Locate data starting at offset

Example: Direct-Mapped Cache

  • Direct mapped: one line per set (E = 1)
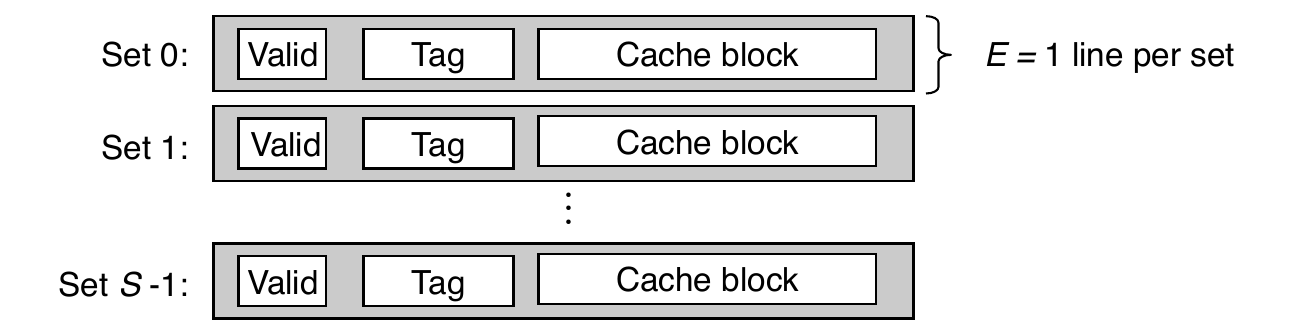
Direct Mapped Cache
Direct Mapped Cache

Example: Direct-Mapped Cache

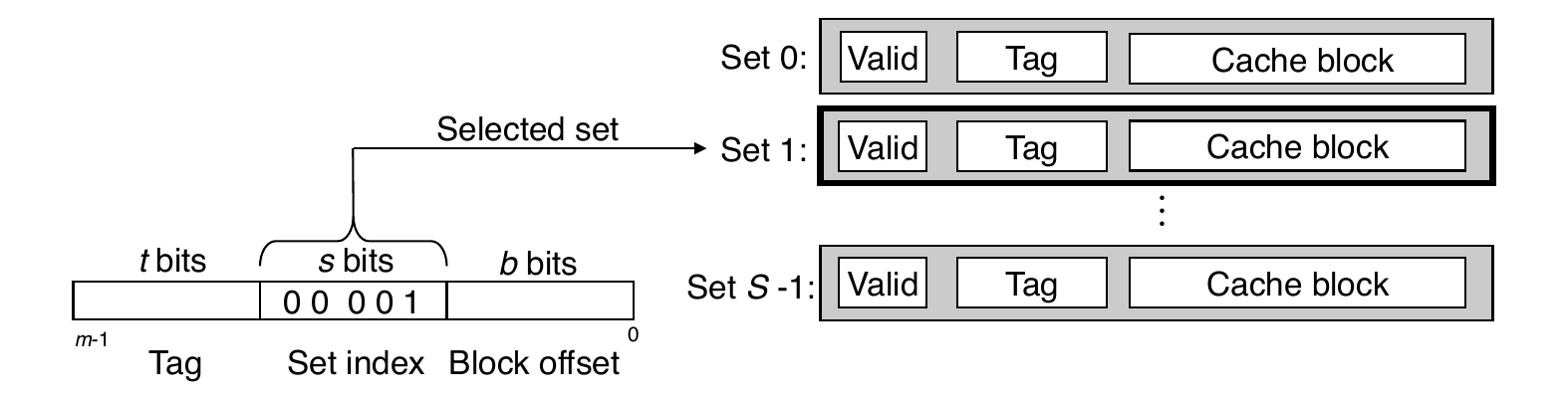
Direct Mapped Cache Index
Direct Mapped Cache Index
  • Note: the middle bits are used for indexing due to better locality

Example: Direct-Mapped Cache

Direct Mapped Cache Match
Direct Mapped Cache Match
  • Note: if tag does not match, then old line is evicted and replaced

Direct-Mapped Cache Simulation

  • Parameters: 4-bit addresses (address space size M = 16 bytes), S = 4 sets, E = 1 Block per set, B = 2 bytes per block

  • Address trace (reads, one byte per read)

    Address t s b Type
    0 0 00 0 miss (cold)
    1 0 00 1 hit
    7 0 11 1 miss (cold)
    8 1 00 0 miss (cold)
    0 0 00 0 miss (conflict)

  • Cache after trace

    Set Valid Tag Block
    0 1 0 M[0-1]
    1 0
    2 0
    3 1 0 M[6-7]

Example: E-way Set Associative Cache

  • There are E lines per set

  • Procedure
    • Find the set with the s-bits
    • Compare the tag for all E lines to the t-bits
    • If any of the tags match, then there is a hit
    • Otherwise, select a line for eviction and replacement from within the set

  • There are many ways to select a replacement: random, least recently used (LRU), etc.

2-way Set Associative Cache Simulation

  • Parameters: 4-bit addresses (address space size M = 16 bytes), S = 2 sets, E = 2 blocks per set, B = 2 bytes per block

  • Address trace (reads, one byte per read)

    Address t s b Type
    0 00 0 0 miss
    1 00 0 1 hit
    7 01 1 1 miss
    8 10 0 0 miss
    0 0i 0 0 hit

  • Cache after trace

    Set Line Valid Tag Block
    0 1 1 00 M[0-1]
    0 2 1 10 M[8-9]
    1 1 1 01 M[6-7]
    1 2 0

Cache Writes

  • Multiple copies of data exist:
    • L1, L2, L3, Main Memory, Disk
  • What to do on a write-hit?
    • Write-through (write immediately to memory)
    • Write-back (defer write to memory until replacement of line)
      • Each cache line needs a dirty bit (set if data differs from memory)
  • What to do on a write-miss?
    • Write-allocate (load into cache, update line in cache)
      • Good if more writes to the location will follow
    • No-write-allocate (writes straight to memory, does not load into cache)
  • Typical combinations
    • Write-through and No-write allocate
    • Write-back and Write-allocate

Intel Core i7 Cache Hierarchy

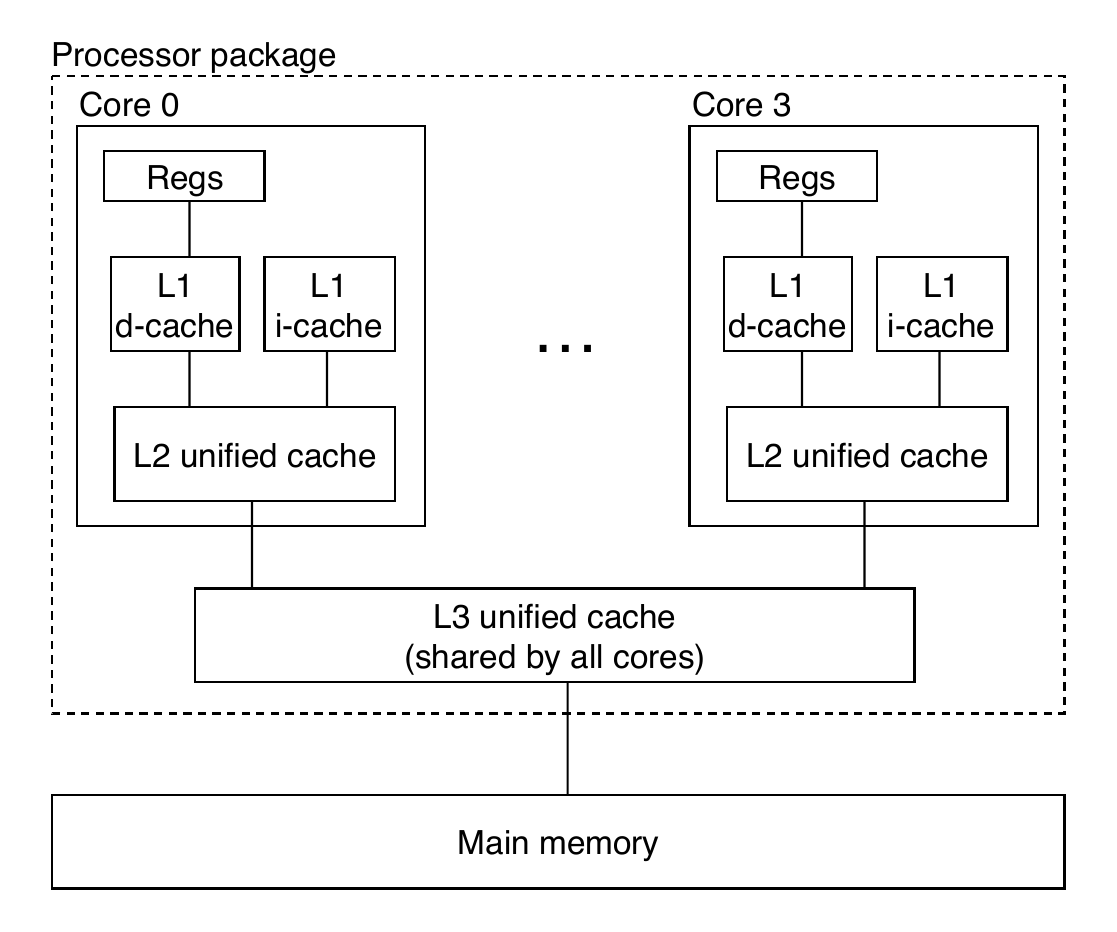
Core i7 Caches
Core i7 Caches

Intel Core i7 Cache Hierarchy

  • L1 i-cache and d-cache:
    • 32 KB, 8-way
    • Access: 4 cycles
  • L2 unified cache:
    • 256 KB, 8-way
    • Access: 10 cycles
  • L3 unified cache:
    • 8 MB, 16-way
    • Access: 40 - 75 cycles
  • Block size: 64 bytes for all caches

Cache Performance Metrics

  • Miss Rate
    • Fraction of memory accesses not found in cache (misses / access)
    • Typical numbers:
      • 3-10% for L1
      • can be quite small for L2, depending on size, etc.
  • Hit Time
    • Time to deliver a cached block to the processor
      • includes time to determine whether line is in cache
    • Typical numbers:
      • 4 clock cycles for L1
      • 10 clock cycles for L2
  • Miss Penalty
    • Additional time required because of a miss
      • typically 50-200 cycles for main memory (trend: increasing)

How Bad Can a Few Cache Misses Be?

  • Huge difference between a hit and a miss
    • Could be 100x if just L1 and main memory
  • Would you believe 99% hits is twice as good as 97%?
    • Consider this simplified example:
      • cache hit time of 1 cycle
      • cache miss penalty of 100 cycles
    • Average access time:
      • 97% hits: 1 cycle + 0.03 \(\times\) 100 cycles = 4 cycles
      • 99% hits: 1 cycle + 0.01 \(\times\) 100 cycles = 2 cycles
  • This is why “miss rate” is used instead of “hit rate”

Writing Cache Friendly Code

  • Make the common case go fast
    • Focus on the inner loops of the core functions
  • Minimize the misses in the inner loops
    • Repeated references to variables are good (temporal locality)
    • Stride-1 reference patterns are good (spatial locality)
  • Key idea: our qualitative notion of locality is quantified through our understanding of cache memories

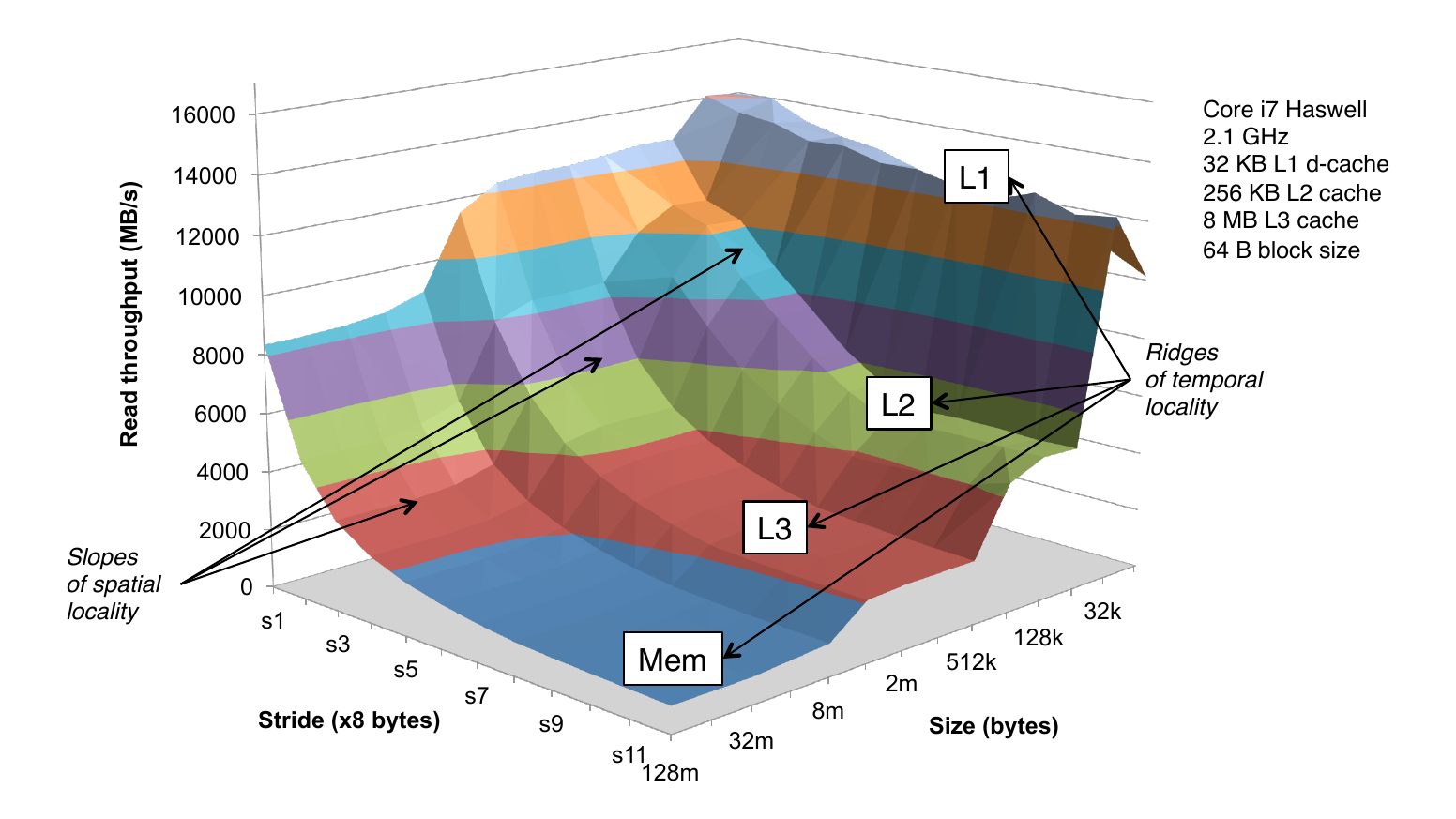
The Memory Mountain

  • Read throughput (read bandwidth)
    • Number of bytes read from memory per second (MB/s)
  • Memory mountain: measured read throughput as a function of spatial and temporal locality
    • Compact way to characterize memory system performance

Memory Mountain Test Function

long data[MAXELEMS];  /* Global array to traverse */

/* test - Iterate over first "elems" elements of
 *        array "data" with stride of "stride“,
 *        using 4x4 loop unrolling.
 */ 
int test(int elems, int stride) {
    long i, sx2=stride*2, sx3=stride*3, sx4=stride*4;
    long acc0 = 0, acc1 = 0, acc2 = 0, acc3 = 0;
    long length = elems, limit = length - sx4;

    /* Combine 4 elements at a time */
    for (i = 0; i < limit; i += sx4) {
        acc0 = acc0 + data[i];
        acc1 = acc1 + data[i+stride];
        acc2 = acc2 + data[i+sx2];
        acc3 = acc3 + data[i+sx3];
    }

    /* Finish any remaining elements */
    for (; i < length; i++) {
        acc0 = acc0 + data[i];
    }
    return ((acc0 + acc1) + (acc2 + acc3));
}

The Memory Mountain

Memory Mountain
Memory Mountain

Matrix Multiplication Example

  • Description:
    • Multiply \(N \times N\) matrices
    • Matrix elements are doubles (8 bytes)
    • \(\mathcal{O}(n^3)\) total operations
    • \(N\) reads per source element
    • \(N\) values summed per destination
      • but may be able to hold in register

Matrix Multiplication Example

  • \(C = A \times B\)
for (i=0; i<n; i++)  {
  for (j=0; j<n; j++) {
    sum = 0.0;
    for (k=0; k<n; k++)
      sum += a[i][k] * b[k][j];
    c[i][j] = sum;
  }
}

Miss Rate Analysis for Matrix Multiply

  • Assume:
    • Block size = 32 B (big enough for doubles)
    • Matrix dimension \(N\) is very large
      • Approximate \(1/N\) as 0.0
    • Cache is not even big enough to hold multiple rows
  • Analysis Method:
    • Look at access pattern of inner loop

Layout of C Arrays in Memory (review)

  • C arrays allocated in row-major order
    • each row in contiguous memory

  • Stepping through columns in one row:

    • Code
    for (i = 0; i < N; i++)
    sum += a[0][i]
    • accesses successive elements
    • if block size \(B > sizeof(a_{ij})\) bytes, then exploit spatial locality
      • miss rate = \(sizeof(a_{ij}) / B\)

  • Stepping through rows in one column:

    • Code
    for (i = 0; i < N; i++)
    sum += a[i][0]
    • accesses distant elements
    • no spatial locality
      • miss rate = 1 (that is, 100%)

Matrix Multiplication (ijk)

for (i=0; i<n; i++)  {
  for (j=0; j<n; j++) {
    sum = 0.0;
    for (k=0; k<n; k++)
      sum += a[i][k] * b[k][j];
    c[i][j] = sum;
  }
}
  • Miss rate for inner loop iterations
    • A = 0.25 (row-wise)
    • B = 1.0 (column-wise)
    • C = 0.0 (fixed)

Matrix Multiplication (kij)

for (k=0; k<n; k++) {
  for (i=0; i<n; i++) {
    r = a[i][k];
    for (j=0; j<n; j++)
      c[i][j] += r * b[k][j];
  }
}
  • Miss rate for inner loop iterations
    • A = 0.0 (fixed)
    • B = 0.25 (row-wise)
    • C = 0.25 (row-wise)

Matrix Multiplication (jki)

for (j=0; j<n; j++) {
  for (k=0; k<n; k++) {
    r = b[k][j];
    for (i=0; i<n; i++)
      c[i][j] += a[i][k] * r;
  }
}
  • Miss rate for inner loop iterations
    • A = 1.0 (column-wise)
    • B = 0.0 (fixed)
    • C = 1.0 (column-wise)

Summary of Matrix Multiplication

  • ijk (and jik)
    • 2 loads, 0 stores
    • average misses per iteration = 1.25
  • kij (and ikj)
    • 2 loads, 1 store
    • average misses per iteration = 0.5
  • jki (and kji)
    • 2 loads, 1 store
    • average misses per iteration = 2.0

Core i7 Matrix Multiply Performance

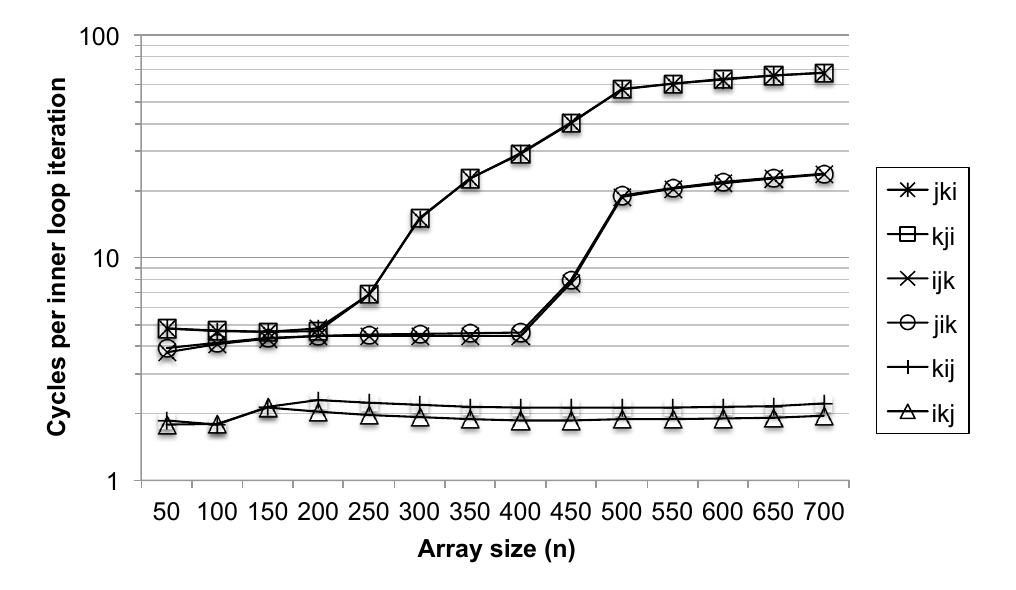
Core i7 Matrix Multiply
Core i7 Matrix Multiply

Matrix Multiplication (Again)

c = (double *) calloc(sizeof(double), n*n);

/* Multiply n x n matrices a and b  */
void mmm(double *a, double *b, double *c, int n) {
    int i, j, k;
    for (i = 0; i < n; i++)
        for (j = 0; j < n; j++)
             for (k = 0; k < n; k++)
                c[i*n + j] += a[i*n + k] * b[k*n + j];
}

Cache Miss Analysis

  • Assume:
    • Matrix elements are doubles
    • Cache line = 8 doubles
    • Cache size is strictly smaller than \(N\)
  • First iteration:
    • \(N/8 + N = 9N/8\) misses
  • Second iteration:
    • \(N/8 + N = 9N/8\) misses
  • Total misses:
    • \(9N/8 N^2 = (9/8) N^3\)

Blocked Matrix Multiplication

c = (double *) calloc(sizeof(double), n*n);

/* Multiply n x n matrices a and b  */
void mmm(double *a, double *b, double *c, int n) {
    int i, j, k;
    for (i = 0; i < n; i+=L)
        for (j = 0; j < n; j+=L)
            for (k = 0; k < n; k+=L)
                  /* L x L mini matrix multiplications */
                  for (i1 = i; i1 < i+L; i1++)
                      for (j1 = j; j1 < j+L; j1++)
                          for (k1 = k; k1 < k+L; k1++)
                              c[i1*n+j1] += a[i1*n + k1]*b[k1*n + j1];
}

Cache Miss Analysis

  • Assume:
    • Cache line = 8 doubles, Blocking size \(L \geq 8\)
    • Cache size is strictly smaller than \(N\)
    • Three blocks fit into cache: \(3L^2 < C\)
  • First (block) iteration:
    • Misses per block: \(L^2/8\)
    • Blocks per iteration: \(2N/L\) (omitting matrix c)
    • Misses per iteration: \(2N/L \times L^2/8 = NL/4\)
    • Afterwards in cache
  • Second (block) iteration:
    • Same misses as first iteration: \(NL/4\)
  • Total misses:
    • \(NL/4\) misses per iteration \(\times\) \((N/L)^2\) iterations = \(N^3/(4L)\) misses

Blocking Summary

  • No blocking: \((9/8) N^3\) misses

  • Blocking: \((1/(4L)) N^3\) misses

  • Use largest block size \(L\), such that \(L\) satisfies \(3L^2 < C\)
    • Fit three blocks in cache: two input, one output
  • Reason for dramatic difference
    • Matrix multiplication has inherent temporal locality:
      • Input data: \(3N^2\), computation \(2N^3\)
      • Every array element used \(\mathcal{O}(n)\) times
    • But, the program needs to be written properly

Cache Summary

  • Cache memories can have significant performance impact

  • You can write your programs to exploit this
    • Focus on the inner loops, where the bulk of computations and memory accesses occur
    • Try to maximize spatial locality by reading data objects sequentially with stride 1
    • Try to maximize temporal locality by using a data object as often as possible once it is read from memory